

Highly nonlinear phenomena in the dynamics of a floating body is one of the important research themes in our section. Numerical computations in this research must be done in the time domain, using mainly Mixed Eulerian Lagrangian (MEL) method. The MEL method makes it possible to satisfy the exact free-surface boundary condition under the assumption of inviscid fluid with irrotational motion. Therefore, this method has been applied to nonlinear water wave probelms and recently being extended to the wave-body interaction problems and more complicated 3-D problems.
The final goal in this study is development of a computer code which can simulate large-amplitude motions of a 3-D body in severe waves.
Right now, we are studying 2-D problems in order to understand fundamental mechanism and get some numerical know-hows.
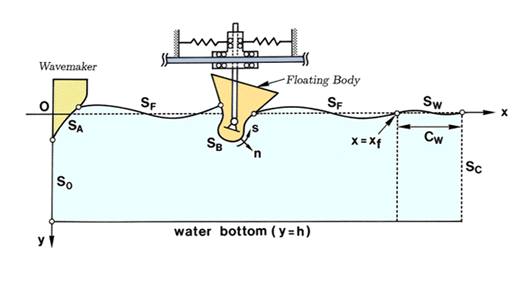
 A numerical method under development is featured in that:
A numerical method under development is featured in that:
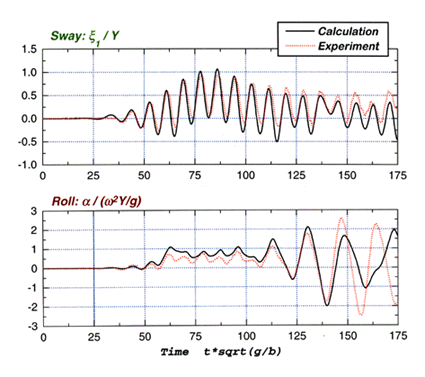
Comparisons with experimental results have been carried out for 1) linear, second- and third-order forces on a 2-D body induced by the forced oscillation test, and 2) the time history of free oscillations of a body in regular waves.
Examples of the results of 2) are shown in the right figure, in which we can see favorable agreement. Extension to 3-D probelms and taking viscous effects into account will be the research topics in the future.
 Link to
related References
Link to
related References
 Home Page of Professor Kashiwagi
Home Page of Professor Kashiwagi
